Berikut ini beberapa latihan soal dan pembahasan materi lingkaran kelas VIII SMP.
Soal 1.
Perhatikan gambar di bawah ini.
Tentukan unsur-unsur yang dapat kita temukan pada gambar tersebut.
Pembahasan:
a. Titik pusat: Titik $A$.
b. Jari-jari lingkaran: $OA$ dan $OB$.
c. Tali busur: $AB$.
d. Apotema: $OC$.
e. Busur: $\overparen{AB}$.
f. Juring:daerah yang dibatasi garis $OA$, $\overparen {AB}$, dan $OB$.
g. Tembereng: daerah yang dibatasi oleh $AB$ dan $\overparen {AB}$.
Soal 2.
Hitunglah keliling dari lingkaran dengan jari-jari berikut.
a. 35 cm
b. 20 cm
Pembahasan:
a. diketahui : $r=35\ cm$
ditanya: keliling = ....
jawab :
Keliling $=2\pi r= 2 \times \frac{22}{7} \times 35 = 2 \times 22 \times 5 =220 cm$
b. diketahui : $r=20\ cm$
ditanya: keliling = ....
jawab :
Keliling $=2\pi r= 2 \times 3,14 \times 20= 6,28 \times 20 =125,6 cm$
Soal 3.
Lingkaran A memiliki keliling 4 cm lebihnya dari lingkaran B. Tentukan selisih jari-jari antara lingkaran A dan lingkaran B.
Pembahasan:
Diketahui: keliling A = 4 + keliling B
Ditanya: $r_A - r_B= ....$
Pembahasan:
Keliling A = 4 + keliling B
$2 \pi r_A = 4 + 2\pi r_B$
$2 \pi r_A - 2\pi r_B = 4$
$2 \pi (r_A - r_B)= 4$
$(r_A - r_B) = \frac{4}{2\pi}$
$(r_A - r_B) = \frac{2}{\pi}$
Soal 4.
Diameter sebuah roda yang berputar adalah 0,56 meter. Tentukan banyaknya putaran roda tersebut pada sebuah jalan dengan panjang 880 meter.
Pembahasan:
Diketahui: d = 0,56 m.
Panjang jalan = 880 m.
Ditanya : banyak putaran roda.
Pembahasan:
$r=\frac{d}{2}=\frac{0,56}{2}=0,28 m =\frac{28}{100}$.
Keliling roda=$2\pi r =2 \times \frac{22}{7} \times \frac{28}{100}=2 \times 22 \times \frac{4}{100}=1,76\ m$.
Banyak putaran roda = $\frac{panjang\ jalan}{keliling\ roda}=\frac{880}{1,76}=500$ putaran.
Soal 5.
Hitunglah luas dari lingkaran dengan jari-jari berikut.
a. 14 cm
b. 10 cm
Pembahasan:
a. diketahui : $r=14\ cm$
ditanya: luas = ....
jawab :
Luas $=\pi r^2= \frac{22}{7} \times 14 \times 14 = 22 \times 2 \times 14= 676\ cm$
b. diketahui : $r=10\ cm$
ditanya: luas = ....
jawab :
Luas $=\pi r^2=3,14 \times 10 \times 10= 3,14\times 100=314\ cm$
Soal 6.
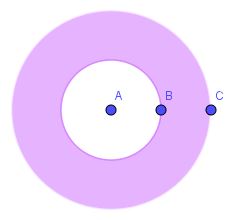
Pada lingkaran di bawah ini, jarak titik A ke B dan titik B ke C adalah 7 cm. Tentukan luas area yang diarsir.
Pembahasan:
Perhatikan bahwa area yang diarsir adalah area lingkaran besar tanpa area lingkaran kecil.
Diketahu: $r_kecil = 7\ cm$
$r_besar = 14\ cm$
Ditanya : luas daerah yang diarsir = ....
Luas lingkaran kecil = $\pi r^2= \frac{22}{7} \times 7 \times 7 = 22 \times 7 =154\ cm^2$
Luas lingkaran besar = $\pi r^2= \frac{22}{7} \times 14 \times 14 = 22 \times 2 \times 14 =616\ cm^2$
Soal 7.
Tentukan luas daerah yang diarsir pada gambar berikut ini jika diketahui panjang persegi tersebut adalah 20 cm.
Pembahasan:
Perhatikan bahwa area yang diarsir ungu adalah area persegi tanpa area lingkaran.
Diketahu: $s = 20\ cm$
$r = 10\ cm$
Ditanya : luas daerah yang diarsir = ....
Luas persegi= $s^2=20^2 = 400\ cm^2$
Luas lingkaran = $\pi r^2= 3,14 \times 10 \times 10 = 314\ cm^2$
Luas daerah yang diarsir ungu = luas persegi - luas lingkaran $= 400 - 314 = 86\ cm^2$
Soal 8.
Tentukan luas daerah yang diarsir pada gambar berikut ini.
Pembahasan:
Perhatikan bahwa gambar tersebut terdiri dari 3 buah lingkaran yaitu lingkaran besar yang berjari-jari 14 cm, lingkaran sedang yang berjari-jari 7 cm, dan lingkaran kecil yang berjari-jari 3,5 cm.
Daerah yang diarsir sendiri adalah gambar lingkaran besar dengan lingkaran kecil, tanpa lingkaran sedang.
$L_{Lingkaran\ besar}=\pi r^2= \frac{22}{7}\times 14 \times 14= 616 cm^2$
$L_{Lingkaran\ sedang}=\pi r^2= \frac{22}{7}\times 7 \times 7= 154 cm^2$
Soal 9.
Pak Adi membuat taman berbentuk lingkaran yang jari-jari 21 m. Keliling taman akan ditanami pohon dengan jarak masing-masing pohon 3 m maka banyak pohon yang dibutuhkan ....
Pembahasan:
Keliling = $2\pi r = 2\cdot \frac{22}{7} \cdot 21 = 2 \cdot 22 \cdot 3 = 132 m$
Banyak pohon= $132 m : 3= 44 pohon $
Soal 1.
Perhatikan gambar di bawah ini.
Tentukan unsur-unsur yang dapat kita temukan pada gambar tersebut.
Pembahasan:
a. Titik pusat: Titik $A$.
b. Jari-jari lingkaran: $OA$ dan $OB$.
c. Tali busur: $AB$.
d. Apotema: $OC$.
e. Busur: $\overparen{AB}$.
f. Juring:daerah yang dibatasi garis $OA$, $\overparen {AB}$, dan $OB$.
g. Tembereng: daerah yang dibatasi oleh $AB$ dan $\overparen {AB}$.
Soal 2.
Hitunglah keliling dari lingkaran dengan jari-jari berikut.
a. 35 cm
b. 20 cm
Pembahasan:
a. diketahui : $r=35\ cm$
ditanya: keliling = ....
jawab :
Keliling $=2\pi r= 2 \times \frac{22}{7} \times 35 = 2 \times 22 \times 5 =220 cm$
b. diketahui : $r=20\ cm$
ditanya: keliling = ....
jawab :
Keliling $=2\pi r= 2 \times 3,14 \times 20= 6,28 \times 20 =125,6 cm$
Soal 3.
Lingkaran A memiliki keliling 4 cm lebihnya dari lingkaran B. Tentukan selisih jari-jari antara lingkaran A dan lingkaran B.
Pembahasan:
Diketahui: keliling A = 4 + keliling B
Ditanya: $r_A - r_B= ....$
Pembahasan:
Keliling A = 4 + keliling B
$2 \pi r_A = 4 + 2\pi r_B$
$2 \pi r_A - 2\pi r_B = 4$
$2 \pi (r_A - r_B)= 4$
$(r_A - r_B) = \frac{4}{2\pi}$
$(r_A - r_B) = \frac{2}{\pi}$
Soal 4.
Diameter sebuah roda yang berputar adalah 0,56 meter. Tentukan banyaknya putaran roda tersebut pada sebuah jalan dengan panjang 880 meter.
Pembahasan:
Diketahui: d = 0,56 m.
Panjang jalan = 880 m.
Ditanya : banyak putaran roda.
Pembahasan:
$r=\frac{d}{2}=\frac{0,56}{2}=0,28 m =\frac{28}{100}$.
Keliling roda=$2\pi r =2 \times \frac{22}{7} \times \frac{28}{100}=2 \times 22 \times \frac{4}{100}=1,76\ m$.
Banyak putaran roda = $\frac{panjang\ jalan}{keliling\ roda}=\frac{880}{1,76}=500$ putaran.
Soal 5.
Hitunglah luas dari lingkaran dengan jari-jari berikut.
a. 14 cm
b. 10 cm
Pembahasan:
a. diketahui : $r=14\ cm$
ditanya: luas = ....
jawab :
Luas $=\pi r^2= \frac{22}{7} \times 14 \times 14 = 22 \times 2 \times 14= 676\ cm$
b. diketahui : $r=10\ cm$
ditanya: luas = ....
jawab :
Luas $=\pi r^2=3,14 \times 10 \times 10= 3,14\times 100=314\ cm$
Soal 6.
Pada lingkaran di bawah ini, jarak titik A ke B dan titik B ke C adalah 7 cm. Tentukan luas area yang diarsir.
Pembahasan:
Perhatikan bahwa area yang diarsir adalah area lingkaran besar tanpa area lingkaran kecil.
Diketahu: $r_kecil = 7\ cm$
$r_besar = 14\ cm$
Ditanya : luas daerah yang diarsir = ....
Luas lingkaran kecil = $\pi r^2= \frac{22}{7} \times 7 \times 7 = 22 \times 7 =154\ cm^2$
Luas lingkaran besar = $\pi r^2= \frac{22}{7} \times 14 \times 14 = 22 \times 2 \times 14 =616\ cm^2$
Soal 7.
Tentukan luas daerah yang diarsir pada gambar berikut ini jika diketahui panjang persegi tersebut adalah 20 cm.
Pembahasan:
Perhatikan bahwa area yang diarsir ungu adalah area persegi tanpa area lingkaran.
Diketahu: $s = 20\ cm$
$r = 10\ cm$
Ditanya : luas daerah yang diarsir = ....
Luas persegi= $s^2=20^2 = 400\ cm^2$
Luas lingkaran = $\pi r^2= 3,14 \times 10 \times 10 = 314\ cm^2$
Luas daerah yang diarsir ungu = luas persegi - luas lingkaran $= 400 - 314 = 86\ cm^2$
Soal 8.
Tentukan luas daerah yang diarsir pada gambar berikut ini.
Pembahasan:
Perhatikan bahwa gambar tersebut terdiri dari 3 buah lingkaran yaitu lingkaran besar yang berjari-jari 14 cm, lingkaran sedang yang berjari-jari 7 cm, dan lingkaran kecil yang berjari-jari 3,5 cm.
Daerah yang diarsir sendiri adalah gambar lingkaran besar dengan lingkaran kecil, tanpa lingkaran sedang.
$L_{Lingkaran\ besar}=\pi r^2= \frac{22}{7}\times 14 \times 14= 616 cm^2$
$L_{Lingkaran\ sedang}=\pi r^2= \frac{22}{7}\times 7 \times 7= 154 cm^2$
$L_{Lingkaran\ kecil}=\pi r^2= \frac{22}{7}\times 3,5 \times 3,5= 38.5 cm^2$
Jadi,
$L_{daerah\ yang\ diarsir}=616+38.5-154=500.5$
Jadi,
$L_{daerah\ yang\ diarsir}=616+38.5-154=500.5$
Soal 9.
Pak Adi membuat taman berbentuk lingkaran yang jari-jari 21 m. Keliling taman akan ditanami pohon dengan jarak masing-masing pohon 3 m maka banyak pohon yang dibutuhkan ....
Pembahasan:
Keliling = $2\pi r = 2\cdot \frac{22}{7} \cdot 21 = 2 \cdot 22 \cdot 3 = 132 m$
Banyak pohon= $132 m : 3= 44 pohon $